Wprowadzenie
Całkowanie numeryczne można porównać do podziału powierzchni całkowanej funkcji na przedziały (im dokładniejszy wynik chcemy uzyskać, tym więcej przedziałów). W zależności od wybranej metody całkowania będziemy liczyć pole w przedziałach dla prostokąta, trapezu lub paraboli. Do wyboru pozostaje nam również wybór czy ewentualny będziemy całkować pole figury pod całkowaną funkcją (z niedomiarem - wtedy uzyskany wynik może być mniejszy niż oczekiwany) lub nad funkcją (z nadmiarem - wtedy oczekiwany wynik może być większy niż oczekiwany). Pod koniec działania programu musimy zsumować pola wszystkich figur z pod przedziałów, które policzyliśmy tak, by uzyskać wynik.
Graficzne przedstawienie problemu
Całkowanie tak prostej funkcji jakmetodą prostokątów może dać duży błąd. Parametry wielkości przedziałów (ich liczność w całkowanym przedziale) należy dobrać odpowiednio tak, by błąd był jak najmniejszy.
Całkowanie funkcji w przedziale od 0 do 8 z podziałem na 4 pod przedziały:
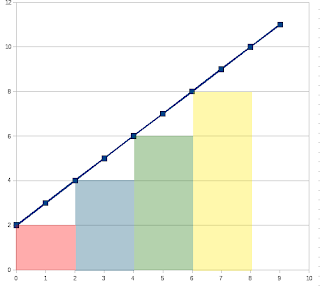
Całkowanie tej samej funkcji metodą trapezów daje wynik bezbłędny nawet przy 1 pod przedziale. Przykład całkowania funkcji y=x+2 w przedziale od 0 do 8 metodą trapezów z 2 pod przedziałami:

Przykład całkowania funkcji nieliniowej y = x * cos(x) metodą trapezów w przedziale od -2 do 2.

Kod programu całkującego metodą trapezów, prostokątów oraz parabol (python 2.x, najlepiej 2.6):
Artykuł udostępniany na licencji CC-BY-SA-3.0

Całkowanie numeryczne można porównać do podziału powierzchni całkowanej funkcji na przedziały (im dokładniejszy wynik chcemy uzyskać, tym więcej przedziałów). W zależności od wybranej metody całkowania będziemy liczyć pole w przedziałach dla prostokąta, trapezu lub paraboli. Do wyboru pozostaje nam również wybór czy ewentualny będziemy całkować pole figury pod całkowaną funkcją (z niedomiarem - wtedy uzyskany wynik może być mniejszy niż oczekiwany) lub nad funkcją (z nadmiarem - wtedy oczekiwany wynik może być większy niż oczekiwany). Pod koniec działania programu musimy zsumować pola wszystkich figur z pod przedziałów, które policzyliśmy tak, by uzyskać wynik.
Graficzne przedstawienie problemu
Całkowanie tak prostej funkcji jakmetodą prostokątów może dać duży błąd. Parametry wielkości przedziałów (ich liczność w całkowanym przedziale) należy dobrać odpowiednio tak, by błąd był jak najmniejszy.
Całkowanie funkcji w przedziale od 0 do 8 z podziałem na 4 pod przedziały:

Całkowanie tej samej funkcji metodą trapezów daje wynik bezbłędny nawet przy 1 pod przedziale. Przykład całkowania funkcji y=x+2 w przedziale od 0 do 8 metodą trapezów z 2 pod przedziałami:

Przykład całkowania funkcji nieliniowej y = x * cos(x) metodą trapezów w przedziale od -2 do 2.

Kod programu całkującego metodą trapezów, prostokątów oraz parabol (python 2.x, najlepiej 2.6):
#!/usr/bin/python
# -*- coding: utf-8 -*-
import math
class Function(object):
def __init__(self):
pass
def count(self,x):
return math.exp(-math.sqrt(x))
def c(self,x):
return self.count(x)
class Zad1Function(Function):
def count(self, x):
return (x+2)
class Zad3FunctionA(Function):
def count(self, x):
return x * math.cos(x)
class Zad3FunctionB(Function):
def count(self, x):
return (math.sin(x) + x**3)
class Zad3FunctionC(Function):
def count(self,x):
return ((x**2) * (math.e**x))
class Calka(object):
def __init__(self,function, a, b,n,method_f="rectangle"):
self.a = a
self.b = b
self.n = n
self.f = function
self.methodF = None
self.setMethodF(method_f)
def setParameters(self, a, b, n,
function = None, method_f=None):
self.a = a
self.b = b
self.n = n
if(function!=None):
self.f = function
if(method_f!=None):
self.setMethodF(method_f)
def setMethodF(self, method_f):
if(method_f == "rectangle"):
self.methodF = self.rectangleField
elif(method_f == "trapezium"):
self.methodF = self.trapeziumField
def setPrecision(self, n):
self.n = n
def rectangleField(self, x0, x1, size):
return min(x1,x0)*size
def trapeziumField(self, x0, x1, size):
return ((x0+x1)*size/2.0)
def parabolaField(self, x1, x2, x3, size):
return (x1+x3+(4*x2))*(size/6)
def printMethodsConfrontation(self):
print "Porownanie metod w przedziale
a: %f b: %f z %f iteracjami"
%(self.a,self.b,self.n)
print "Metoda Prostokatow: %f " %(self.count("ractangle"))
print "Metoda Trapezow : %f " %(self.count("trapezium"))
print "Metoda Parabol : %f " %(self.parabolaCount())
def count(self, method=None):
if(method!=None):
self.setMethodF(method)
size = (self.b-self.a)/self.n
x0 = float(self.a)
x2 = math.fabs(self.f.c(x0))
result = 0.0
for i in range(int(self.n)):
x1 = x2
x0 = x0 + size
x2 = math.fabs(self.f.c(x0))
result += self.methodF(x1,x2,size)
return result
def parabolaCount(self):
size = (float(self.b)-float(self.a))/float(self.n)
x0 = float(self.a)
x3 = math.fabs(self.f.c(x0))
result = 0.0
for i in range(int(self.n)):
x1 = x3
x2 = math.fabs(self.f.c(x0 + size/2.0))
x3 = math.fabs(self.f.c(x0 + size))
result += self.parabolaField(x1,x2,x3,size)
x0 += size
return result
func = Zad1Function()
calka = Calka(func,0.0, math.pi,315.0)
print "Funkcja 1: "
calka.printMethodsConfrontation()
calka.f = Zad3FunctionA()
print "Funkcja 3a: "
calka.printMethodsConfrontation()
calka.f = Zad3FunctionB()
print "Funkcja 3b: "
calka.b = 3 * math.pi
calka.printMethodsConfrontation()
calka.f = Zad3FunctionC()
print "Funkcja 3c: "
calka.b = 1.0
calka.printMethodsConfrontation() Schemat pracy w/w algorytmu przedstawia się następująco: Artykuł udostępniany na licencji CC-BY-SA-3.0


Bardzo przydatna strona ;-) Na informatyce mam właśnie obliczanie pola pod krzywą ...
OdpowiedzUsuń